Whats the Square Root of 3500 to the Second Power

Our square root calculator estimates the square root of whatsoever positive number you want. Just enter the called number and read the results. Everything is calculated quickly and automatically! With this tool, you can as well estimate the foursquare of the desired number (just enter the value into the 2nd field) which may exist a great aid in finding perfect squares from the foursquare root formula.

Are you struggling with the basic arithmetic operations: adding square roots, subtracting square roots, multiplying foursquare roots or dividing square roots? Non any more! In the post-obit text, you volition notice a detailed explanation near different square root properties, e.g., how to simplify foursquare roots, with many various examples given. With this article, yous will learn once and for all how to find square roots!

Have you lot ever wondered what is the origin of the square root symbol √? Nosotros can assure you that this history is not equally simple every bit you might think at commencement. The origin of the root symbol goes dorsum to ancient times, as the origin of the percent sign.

If yous're looking for the square root graph or square root office properties, head straight to the advisable section (merely click the links higher up!). In that location, nosotros explain what is the derivative of a square root using a fundamental square root definition; we too elaborate on how to calculate square roots of exponents or foursquare roots of fractions. Finally, if you are persistent plenty, you will discover out that foursquare root of a negative number is, in fact, possible. In that manner, we introduce circuitous numbers which detect broad applications in physics and mathematics.

Foursquare root symbol √

The operation of the square root of a number was already known in antiquity. The earliest clay tablet with the correct value of upwardly to 5 decimal places of √ii = 1.41421 comes from Babylonia (1800 BC - 1600 BC). Many other documents show that foursquare roots were also used by the ancient Egyptians, Indians, Greeks, and Chinese. However, the origin of the root symbol √ is still largely speculative.

many scholars believe that square roots originate from the letter "r" - the start letter of the Latin discussion radix significant root,
another theory states that square root symbol was taken from the Arabic alphabetic character ج that was placed in its original class of ﺟ in the word جذر - root (the Arabic language is written from right to left).

The first use of the square root symbol √ didn't include the horizontal "bar" over the numbers inside the square root (or radical) symbol, √‾. The "bar" is known every bit a vinculum in Latin, meaning bail. Although the radical symbol with vinculum is now in everyday use, we usually omit this overline in the many texts, like in manufactures on the internet. The notation of the higher degrees of a root has been suggested by Albert Girard who placed the degree index within the opening of the radical sign, due east.g., ³√ or ⁴√.

The terminal question is why is the foursquare root operation called root regardless of its true origin? The caption should become more evident if we write the equation x = ⁿ√a in a different form: xⁿ = a. x is called a root or radical because it is the hidden base of a. Thus, the word radical doesn't mean far-reaching or farthermost, but instead foundational, reaching the root cause.

Foursquare root definition

In mathematics, the traditional operations on numbers are addition, subtraction, multiplication, and partitioning. Notwithstanding, we sometimes add together to this list some more advanced operations and manipulations: square roots, exponentiation, logarithmic functions and even trigonometric functions (e.g., sine and cosine). In this commodity, we will focus on the foursquare root definition merely.

The square root of a given number x is every number y whose foursquare y² = y*y yields the original number ten. Therefore, the square root formula can exist expressed equally:

√10 = y ⟺ x = y²,

where ⟺ is a mathematical symbol that means if and only if. Each positive real number always has ii square roots - the outset is positive and 2d is negative. However, for many applied purposes, we usually use the positive i. The only number that has one foursquare root is nil. It is because √0 = 0 and zip is neither positive nor negative.

There is also another common notation of square roots that could be more convenient in many circuitous calculations. This alternative square root formula states that the square root of a number is a number raised to the exponent of the fraction one one-half:

√x = x^(1/2) = x^(0.5)

🔎 Is 1/ii a fraction or a ratio? Or maybe both? Learn the divergence with our ratio figurer!

In geometric interpretation, the square root of a given surface area of a square gives the length of its side. That'due south why √ has word square in its name. A similar situation is with the cube root ∛. If you take the cube root of the book of a cube, yous get the length of its edges. While square roots are used when because surface areas, cube roots are useful to make up one's mind quantities that relate to the volume, e.g., density.

How to find the square root?

Mayhap we aren't being very minor, just nosotros think that the all-time answer to the question how to observe the square root is straightforward: utilize the square root reckoner! You lot can use it both on your computer and your smartphone to quickly gauge the foursquare root of a given number. Unfortunately, there are sometimes situations when you tin can rely only on yourself, what then? To set for this, you should remember several bones perfect square roots:

square root of one: √1 = 1, since one * 1 = 1;
foursquare root of 4: √4 = 2, since 2 * 2 = 4;
square root of ix: √ix = 3, since iii * iii = 9;
square root of 16: √16 = 4, since 4 * 4 = 16;
foursquare root of 25: √25 = 5, since 5 * 5 = 25;
square root of 36: √36 = 6, since 6 * 6 = 36;
foursquare root of 49: √49 = 7, since 7 * 7 = 49;
foursquare root of 64: √64 = 8, since 8 * 8 = 64;
foursquare root of 81: √81 = 9, since 9 * 9 = 81;
foursquare root of 100: √100 = 10, since 10 * 10 = 100;
square root of 121: √121 = eleven, since 11 * 11 = 121;
square root of 144: √144 = 12, since 12 * 12 = 144;

The in a higher place numbers are the simplest square roots considering every time y'all obtain an integer. Try to remember them! Only what can y'all do when there is a number that doesn't have such a nice square root? In that location are multiple solutions. First of all, y'all tin can try to predict the issue by trial and fault. Let's say that y'all desire to approximate the foursquare root of 52:

You know that √49 = vii and √64 = viii and then √52 should be betwixt 7 and viii.
Number 52 is closer to the 49 (finer closer to the 7) and so y'all tin can try guessing that √52 is 7.3.
Then, y'all square 7.3 obtaining seven.3² = 53.29 (as the square root formula says) which is higher than 52. You have to try with a smaller number, allow'due south say seven.2.
The foursquare of seven.2 is 51.84. At present y'all have a smaller number, but much closer to the 52. If that accuracy satisfies you, you can end estimations here. Otherwise, you tin repeat the procedure with a number chosen between vii.two and 7.3,e.k., 7.22 then on and so along.

Another approach is to simplify the square root start and then employ the approximations of the prime numbers foursquare roots (typically rounded to 2 decimal places):

square root of 2: √ii ≈ i.41,
foursquare root of 3: √3 ≈ i.73,
square root of 5: √v ≈ 2.24,
square root of seven: √7 ≈ ii.65,
square root of 11: √11 ≈ iii.32,
foursquare root of thirteen: √13 ≈ 3.61,
foursquare root of 17: √17 ≈ 4.12,
foursquare root of xix: √xix ≈ four.34, etc.

Let's try and find the square root of 52 over again. You can simplify information technology to √52 = 2√13 (you volition learn how to simplify square root in the next section) and so substitute √thirteen ≈ 3.61. Finally, make a multiplication √52 ≈ 2 * 3.61 = vii.22. The result is the same every bit before!

Yous can cheque whether a number is prime or not with our prime calculator. A prime number is a natural number (greater than 1) that can't be obtained every bit a product of two smaller natural numbers. For case, 7 is a prime number considering you tin become it but past multiplying i * 7 or 7 * ane. On the other manus, number 8 is not prime number, considering yous tin form it by multiplying 2 * 4 or iv * ii (besides production of 1 and 8 itself).

Square root calculator

In some situations, you don't need to know the verbal result of the foursquare root. If this is the case, our foursquare root reckoner is the best choice to estimate the value of every square root you lot desired. For example, let'southward say y'all desire to know whether iv√5 is greater than ix. From the figurer, yous know that √5 ≈ 2.23607, so iv√5 ≈ 4 * 2.23607 = 8.94428. Information technology is very close to the 9, but it isn't greater than it! The square root calculator gives the final value with relatively high accuracy (to v digits in above example). With the pregnant figure figurer, you can calculate this result to equally many significant figures every bit you lot want.

Remember that our calculator automatically recalculates numbers entered into either of the fields. You lot can find what is the square root of a specific number by filling the beginning window or become the square of a number that you entered in the second window. The second option is handy in finding perfect squares that are essential in many aspects of math and science. For case, if y'all enter 17 in the second field, you will observe out that 289 is a perfect square.

In some applications of the square root, particularly those pertaining to sciences such as chemistry and physics, the results are preferred in scientific note. In brief, an answer in scientific notation must accept a decimal point between the get-go ii non-zero numbers and will exist represented as the decimal multiplied by x raised to an exponent. For case, the number 0.00345 is written equally 3.45 * x⁻³ in scientific notation, whereas 145.67 is written as 1.4567 * ten² in scientific note. The results obtained using the square root reckoner tin be converted to scientific notation with the scientific notation calculator.

How to simplify foursquare roots?

Outset, permit'southward ask ourselves which square roots can exist simplified. To answer it, you need to take the number which is after the foursquare root symbol and discover its factors. If whatever of its factors are square numbers (four, 9, 16, 25, 36, 49, 64 and so on), then you tin can simplify the square root. Why are these numbers square? They can be respectively expressed as 2², three², four², 5², vi², 7² and and then on. According to the square root definition, you can call them perfect squares. We've got a special tool chosen the gene calculator which might be very handy here. Allow'south take a look at some examples:

tin can you simplify √27? With the calculator mentioned above, you obtain factors of 27: 1, iii, 9, 27. In that location is 9 here! This ways you can simplify √27.
tin can you simplify √15? Factors of 15 are ane, 3, 5, 15. There are no perfect squares in those numbers, so this foursquare root tin't be simplified.

And so, how to simplify foursquare roots? To explain that, nosotros will utilize a handy square root property we have talked about earlier, namely, the alternative square root formula:

√x = x^(ane/2)

We tin can use those ii forms of square roots and switch between them whenever we want. Particularly, nosotros recollect that power of multiplication of two specific numbers is equivalent to the multiplication of those specific numbers raised to the same powers. Therefore, we can write:

(x * y)^(1/2) = x^(1/ii) * y^(one/2) ⟺ √(x * y) = √ten * √y,

How tin can you lot use this cognition? The argument of a square root is usually not a perfect square y'all can easily calculate, but it may contain a perfect square amongst its factors. In other words, you lot can write it as a multiplication of two numbers, where ane of the numbers is the perfect square, e.g., 45 = 9 * 5 (9 is a perfect square). The requirement of having at to the lowest degree one factor that is a perfect foursquare is necessary to simplify the square root. At this bespeak, you should probably know what the next step volition exist. Yous demand to put this multiplication under the foursquare root. In our example:

√45 = 45^(i/2) = (9 * 5)^(1/two) = 9^(1/two) * five^(1/2) = √nine * √5 = 3√5.

Yous have successfully simplified your first foursquare root! Of grade, you don't have to write down all these calculations. Every bit long as you call up that square root is equivalent to the power of one half, you can shorten them. Let's do simplifying square roots with another examples:

How to simplify square root of 27? √27 = √(9 * 3) = √9 * √3 = iii√three;
How to simplify square root of 8? √viii = √(4 * 2) = √four * √2 = 2√ii;
How to simplify foursquare root of 144? √144 = √(4 * 36) = √4 * √36 = two * 6 = 12.

In the last instance, you didn't have to simplify the foursquare root at all, considering 144 is a perfect square. You could merely recollect that 12 * 12 = 144. However, we wanted to show you lot that with the process of simplification, you tin can easily calculate square roots of perfect squares too. It is useful when dealing with big numbers.

Finally, you may ask how to simplify roots of higher orders, e.g., cube roots. In fact, the procedure is very analogical to the square roots, but in the case of cube roots, you have to find at least 1 factor that is a perfect cube, not a perfect square, i.e., viii = 2³, 27 = iii³, 64 = four³, 125 = 5³ and and so on. Then you lot divide your number into two parts and put under the cube root. Permit's take the post-obit example of simplifying ³√192:

∛192 = ∛(64 * 3) = ∛64 * ∛3 = 4∛3

It may seem a picayune bit complicated at outset glance, only afterward some practise, you will be able to simplify roots in your head. Trust u.s.a.!

Adding, subtracting, multiplying and dividing square roots

Adding square roots and subtracting foursquare roots

Unfortunately, adding or subtracting square roots are not as easy as adding/subtracting regular numbers. For instance, if 2 + 3 = v, it doesn't mean that √ii + √3 equals √5. That's wrong! To understand why is that, imagine that you have two dissimilar types of shapes: triangles 🔺 and circles 🔵. What happens when you add one triangle to one circumvolve 🔺 + 🔵? Cypher! You yet have ane triangle and one circle 🔺 + 🔵. On the other hand, what happens when you try to add iii triangles to v triangles: 3🔺 + five🔺? Y'all'll we go 8 triangles 8🔺.

Calculation square roots is very like to this. The result of adding √two + √iii is still √2 + √3. Yous can't simplify it further. It is a unlike situation however when both foursquare roots have the aforementioned number nether the root symbol. Then we can add together them just as regular numbers (or triangles). For case 3√two + 5√2 equals 8√2. The same thing is truthful subtracting square roots. Let's take a await at more examples illustrating this square root property:

What is half dozen√17 + 5√17? Reply: 6√17 + 5√17 = xi√17;
What is iv√vii - 7√vii? Answer: 4√7 - 7√vii = -three√seven;
What is 2√2 + 3√eight? Answer: 2√ii + 3√viii = 2√ii + six√ii = 8√2, because we simplified √eight = √(iv * 2) = √four * √2 = 2√ii;
What is √45 - √20? Answer: √45 - √20 = iii√five - 2√five = √5, considering nosotros simplified √45 = √(9 * 5) = √nine * √5 = 3√5 and √20 = √(iv * v) = √4 * √v = two√v;
What is 7√thirteen + 2√22? Answer: 7√xiii + 2√22, nosotros can't simplify this further;
What is √3 - √18? Reply: √3 - √18 = √3 - three√2, nosotros can't simplify this further than this, but we at to the lowest degree simplified √18 = √(9 * 2) = √9 * √two = 3√2.

Multiplying foursquare roots and dividing square roots

At present, when calculation square roots is a piece of cake for you, permit's go ane step further. What near multiplying square roots and dividing foursquare roots? Don't be scared! In fact, you already did it during the lesson of simplifying square roots. Multiplying square roots is based on the foursquare root property that we have used earlier a few times, that is:

√10 = ten^(1/ii)

Exercise you recall how to multiply numbers that are raised to the same power? As a reminder:

xⁿ * yⁿ = (x * y)ⁿ,

and therefore

x^(1/2) * y^(1/ii) = (x * y)^(i/two) ⟺ √10 * √y = √(x * y).

Equally opposed to add-on, y'all can multiply every 2 square roots. Recall that multiplication has commutative properties, that means that the order to which 2 numbers are multiplied does not matter. Few examples should clarify this issue:

What is √3 * √2? Answer: √3 * √2 = √half-dozen;
What is 2√5 * 5√iii? Respond: two√5 * five√3 = ii * five * √5 * √3 = x√15, because multiplication is commutative;
What is 2√six * 3√three? Respond: 2√half-dozen * 3√three = 2 * 3 * √6 * √3 = half dozen√18 = 18√3, we simplified √18 = √(9 * ii) = √9 * √2 = 3√two.

Dividing square root is almost the same since:

ten^(1/2) / y^(1/2) = (x / y)^(1/ii) ⟺ √x / √y = √(x / y).

All you need to practise is to replace multiplication sign with a partitioning. However, the sectionalization is not a commutative operator! You have to summate the numbers that stand before the square roots and numbers under the square roots separately. As always, some applied examples:

What is √15 / √3? Answer: √fifteen / √three = √5;
What is ten√half-dozen / v√ii? Answer: 10√half-dozen / 5√ii = (ten / 5) * (√6 / √2) = 2√three;
What is six√ii / 3√five? Answer: half-dozen√two / 3√5 = (six / 3) * (√2 / √5) = 2√(two/5) = 2√(0.4), we switched at that place from a simple fraction 2/five to the decimal fraction ii/5 = 4/10 = 0.4.

Square roots of exponents and fractions

Calculating the foursquare root of the exponent or square root of the fraction might not be clear for y'all. But with the knowledge you acquired in the previous section, you should find it easier than you expected! Let'due south begin with the square roots of exponents. In that example, it will exist easier for y'all to apply the alternative form of square root √x = x^(1/2). Practice yous remember the power rule? If non, here is a quick reminder:

(x^n)^chiliad = ten^(northward*m),

where north and m are whatever existent numbers. Now, when yous place 1/2 instead of m yous'll go zero else but a square root:

√(x^n) = (ten^northward)^(ane/two) = x^(northward/2),

and that's how you detect the square root of an exponent. Speaking of exponents, to a higher place equation looks very similar to the standard normal distribution density role, which is widely used in statistics.

If you're however not sure virtually taking square roots of exponents, here are a few examples:

square root of ii^4: √(ii^4) = (two^4)^(ane/2) = 2^(4/2) = ii^ii = 4,
foursquare root of 5^3: √(5^three) = (5^three)^(i/2) = five^(3/ii),
square root of iv^five: √(4^v) = (4^five)^(1/two) = four^(v/2) = (2^2)^(5/2) = two^v = 32.

As y'all tin can see, sometimes it is incommunicable to get a pretty result like the first example. However, in the third example, we showed y'all a little trick with expressing 4 every bit ii^2. This arroyo can often simplify more than complicated equations.

What about foursquare roots of fractions? Take a look at the previous section where nosotros wrote about dividing square roots. You can find there the following relation that should explain everything:

(x / y)^(1/two) ⟺ √x / √y = √(10 / y),

where ten / y is a fraction. Below you can find some examples of square roots of a fraction:

square root of 4/9: √(4/9) = √4 / √nine = 2/three,
foursquare root of i/100: √(1/100) = √ane / √100 = 1/ten,
square root of 1/5: √(1/5) = √1 / √5 = 1/√5 = √5/5.

Leaving roots in the denominator is not a very skillful habit. That'south why we got rid of information technology in the last example. Nosotros simply multiplied both the numerator and denominator by the same number (we can always do that, as the number we multiply by equals 1), in this instance by √5.

Foursquare root function and graph

Functions play a vital role not only in mathematics but in many other areas like physics, statistics, or finance. Function f(x) is zip more than a formula that says how the value of f(x) changes with the statement x. To see some examples, cheque out our finance tools fabricated by financial specialists, for example, the compound interest calculator or future value calculator. You will notice there some functions that you can employ in existent life. They're a bang-up help if you want to know how to calculate the compound interest or to approximate the future value of an annuity.

Below yous can find the square root graph, made up of half of a parabola. Check it and effort to validate, for instance, whether the square root function of 10 = 9 is 3 and of x = 16 is four (every bit it should be).

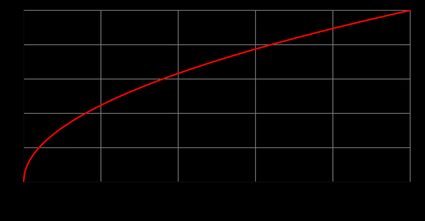
Square root function (square root graph)

Let's get back to the square root function f(x) = √x and explore what are its basic properties. Nosotros consider there merely the positive part of f(x) (as yous can see in the square root graph to a higher place). So, the foursquare root function:

is continuous and growing for all not-negative x,
is differentiable for all positive x (run into the derivative of the square root section for more information),
approaches the limit of infinity as x approaches infinity (lim √x → ∞ when x → ∞),
is a existent number for all non-negative x and a complex number for all negative x (nosotros write more than about it in the square root of a negative number department).

You probably have already noticed that the square root of the area of a square gives its side length. This feature is used in ane of our construction calculators - square footage figurer. If yous program to do whatever renovation in the future, these tools might be a great help. Don't forget to use them!

Derivative of the square root

A derivative of a function tells us how fast this function changes with its statement. One of the simplest examples in physics is the position of an object and its velocity (the rate of modify of position). Allow'south say that the function x(t) describes how the distance of the moving car from a specific point changes with time t. Practise you know what determines how fast the modify is in your altitude traveled? The answer is the speed of the car! Then the derivative of the position ten(t) is velocity five(t)(velocity can depend on time too). To denote derivative, we usually use apostrophe v(t) = x'(t) or the derivative symbol v(t) = dx(t)/dt.

The derivative of the general function f(x) is not always easy to summate. However, in some circumstances, if the function takes a specific form, we've got some formulas. For example, if

f(ten) = x^n,

where due north is whatsoever existent number, the derivative is every bit follows:

f'(x) = north * x^(northward-1).

Information technology may not look like, but this answers the question what is the derivative of a square root. Exercise you retrieve the alternative (exponential) class of a square root? Let u.s.a. remind you:

√ten = x^(ane/2).

Yous can encounter that in this case n = 1/2, so the derivative of a square root is:

(√ten)' = (x^(1/ii))' = 1/2 * ten^(-i/2) = 1/(2√x).

Since a number to a negative ability is ane over that number, the interpretation of the derivation will involve fractions. We've got a tool that could be essential when calculation or subtracting fractions with different denominators. It is called the LCM reckoner, and information technology tells you how to detect the Least Common Multiple.

The derivative of a square root is needed to obtain the coefficients in the so-chosen Taylor expansion. We don't want to dive into details as well deeply, so, briefly, the Taylor serial allows you to gauge various functions with the polynomials that are much easier to calculate. For example, the Taylor expansion of √(1 + x) most the betoken x = 0 is given past:

√(1 + x) = one + i/ii * x - 1/viii * ten² + 1/16 * x³ - five/128 * x⁴ + ...,

which is valid for -one ≤ 10 ≤ one. Although the above expression has an infinite number of terms, to become the approximate value you tin use but a few get-go terms. Let'southward effort it! With x = 0.5 and first 5 terms, you get:

√(ane.5) = 1 + one/two * 0.5 - 1/8 * 0.25 + 1/16 * 0.125 - v/128 * 0.0625,

√(1.5) ≈ 1.2241,

and the real value, provided by our computer, is √(1.5) ≈ i.2247. Close enough!

That was a lot of maths and equations so far. For those of you who are persistent enough, we've prepared the side by side section which explains how to calculate the foursquare root of a negative number.

Square root of a negative number

At school, you lot probably accept been taught that square root of a negative number does not exist. This is true when you consider but real numbers. A long time ago, to perform advanced calculations, mathematicians had to innovate a more general set of numbers - the complex numbers. They can be expressed in the post-obit form:

x = a + b*i,

where x is the circuitous number with the real part a and imaginary part b. What differs between a complex number and a existent one is the imaginary number i. Here yous have some examples of complex numbers: 2 + 3i, 5i, 1.5 + 4i, two. You may exist surprised seeing 2 at that place which is a existent number. Yeah, information technology is, just it is also a complex number with b = 0. Complex numbers are a generalization of the existent numbers.

Then far imaginary number i is probably notwithstanding a mystery for y'all. What is it at all? Well, although it may wait weird, it is divers past the post-obit equation:

i = √(-one),

and that's all that you need to summate the square root of every number, whether it is positive or non. Let's see some examples:

square root of -nine: √(-9) = √(-1 * ix) = √(-1)√9 = 3i,
square root of -13: √(-thirteen) = √(-one * 13) = √(-ane)√13 = i√xiii,
foursquare root of -49: √(-49) = √(-1 * 49) = √(-1)√49 = 7i.

Isn't that simple? This problem doesn't arise with the cube root since you can obtain the negative number by multiplying three of the identical negative numbers (which you tin can't do with two negative numbers). For example:

³√(-64) = ³√[(-iv)*(-iv)*(-4)] = -4.

That's probably everything you should know about square roots. We appreciate that you stayed with u.s. until this point! As a reward yous should bake something sweet for yourself :-) Check out our perfect pancake calculator to find out how to make the perfect pancake, all the same y'all like information technology. You may need our grams to cups computer to help you lot with this. It works both ways, i.eastward., to convert grams to cups and convert cups to grams. And if you ask yourself "How many calories should I eat a day?", visit our handy calorie calculator!

FAQ

Can a number have more than one square root?

Yes, in fact all positive numbers accept 2 foursquare roots, i that is positive and another that is equal only negative to the first. This is because if you multiply ii negatives together, the negatives cancel and the result is positive.

How practise you find the square root without a calculator?

Brand an estimate of the square root. The closest square number is acceptable if you're at a loss.
Split up the number you desire to find the square root of by the estimate.
Add the estimate to the result of step two.
Dissever the result of stride 3 by 2. This is your new approximate.
Echo steps 2-4 with y'all new approximate. The more times this is repeated, the more than authentic the result is.

How tin I estimate square roots?

Find the nearest foursquare number above and below the number you are thinking of.
The foursquare root will exist between the square roots of these numbers.
The closeness of the number to a square root indicates how shut the root is. E.g., 26 is very close to 25, then the root will be very shut to 5.
Try a few times to become the hang of it.

Is the square root of two a rational number?

No, the foursquare root of 2 is not rational. This is because when 2 is written as a fraction, ²/₁, it can never have only even exponents, and therefore a rational number cannot have been squared to create information technology.

How can I get rid of a foursquare root?

In algebra, squaring both sides of the equation will get rid of any square roots. The effect of this operation is that the square roots volition exist replaced with any number they were finding the square root of.

Are square roots rational?

Some square roots are rational, whereas others are non. You lot tin work out if a foursquare root is rational or not past finding out if the number you are square rooting can be expressed in terms of only even exponents (e.g. iv = 2ⁱⁱ / i ²). If it tin, its root is rational.

Is the square root of v a rational number?

The square root of v is not a rational number. This is because v cannot be expressed as a fraction where both the numerator and denominator have even exponents. This ways that a rational number cannot take been squared to get 5.

Is the square root of 7 a rational number?

The result of square rooting seven is an irrational number. seven cannot be written as a fraction with only even exponents, pregnant that the number squared to reach 7 cannot be expressed as a fraction of integers, and therefore is not rational.

What is the derivative of the square root of ten?

The derivative of square root x is ^{ten^{-^one/₂}}/₂, or ¹/_2SQRT(x). This is because the square root of x can exist expressed every bit x^¹/₂, from which differentiation occurs normally.

How practise you lot notice the foursquare root of a decimal?

Convert the decimal into a fraction.
Find any foursquare roots of the fraction, or estimate it. Brand the fraction equal to the square root you lot found squared.
Cancel the foursquare root and the square leaving you with the fraction.
Rewrite the fraction every bit a decimal as your final reply.

Dominik Czernia , PhD candidate

Absolute value Improver Associative property … 53 more

killiansath1996.blogspot.com

Source: https://www.omnicalculator.com/math/square-root